We are running a campaign to offer a certain product to a customer. An offer obviously may not be accepted at the first trial, so each customer can be offered the same product several times up to, say, six times, or until he/she accepted the offer.
From the marketer’s perspective, if they send an offer to a customer and then the customer rejects it, it can be counted as a “failure”. So the marketer can “fail” multiple times before their offer is accepted by a customer, which will be a “success” for them.

Source: freshwatervacationrentals.com
Let’s check how many customers accepted an offer in the \(k^{th}\) campaign.
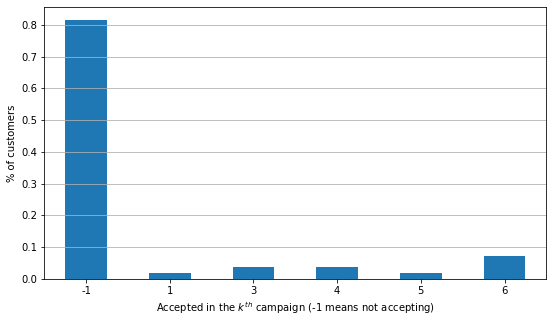
The probability of accepting a campaign offer in a \(k^{th}\) campaign is varied. But in general, the probability of accepting a campaign offer by any customer in any \(k^{th}\) campaign is 18.49% (because the probability of the opposite is around 81.51%). It’s a quite good acceptance rate, but again, it broadly tells the probability of accepting an offer, not by a particular customer or in a particular campaign.
Meanwhile in one scenario, we’d like to see the probability of accepting an offer in a particular \(k^{th}\) campaign after knowing that the probability of acceptance in general is 18.49%.
We will try to model this with Geometric Distribution.
By approaching this problem with Geometric Distribution, we rather put interest toward the probability of having \(k\) campaigns rejected by a customer before finally accepted. It should be the same probability as before, just in a different sentence. The difference will be on how we construct the probability distribution.
Assume for now that every campaign offer to a customer is a Bernoulli trial and the probability of accepted is the same for every trial. So the random variable will be about how many failed Bernoulli trials attempted before a success.
We define the probability mass function as
\[Pr(X = k) = (1 - p)^kp\]
This function will help us to find the probability of having \(k\) rejected offers before the accepted one, having known the probability of accepted offer \(p\).
By plugging in our \(p\) and every \(k\) from our data, here is our distribution.
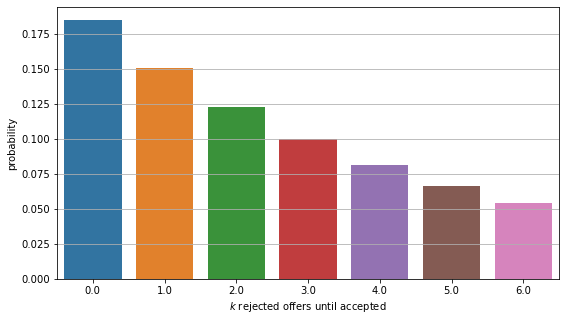
As more trials are done, the probability of having failed campaigns of the trial number is lower. The customers are more likely to accept an offer after only offered by few campaigns.
.
.
.
But, wait. What could be wrong?
The probability of success is assumed to be the same on every \(k^{th}\) campaign, while the actual case can be different, as we saw at the very first barplot. Thus, the trials could be dependent with each other, i.e. the chance of accepting may be higher if the customer has refused the offer few times before.
Having said that, the issue here is we cannot use only single \(p\) to represents the probability of accepted campaign. Different \(k\) could have different \(p\).
So what would be the alternative? Perhaps, a distribution family like Geometric but with different \(p\) for each trial (e.g. a distribution with something like \(p_k\) parameter). So far, I haven’t found such distribution family that is more suitable for our problem.
My first search on Google with keywords “geometric distribution with different probability of success for each trial” led me to this StackExchange page, but no promising answer until now. One of the users did said that such distribution could exist but without any specific name.
Or, if we want to do a little bit of conditional probability:
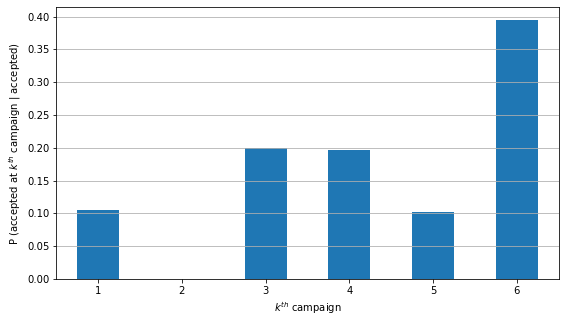
Another PMF plot? Errr nope. Actually the plot above is the same as the first one, except we don’t include the probability of not accepting. The probability of each \(k\) changes though, but no any additional insight because there isn’t such case as “accepted at \(k^th\) campaign given the customer rejects the offer”.
After all, it’s rather counterintuitive to compute the probability of acceptance in each particular \(k^{th}\) campaign, even after seeing the barplot above.